Brian's brain on Clojure

A couple weeks ago I came across a blog entry by Lau B. Jensen about Brian's Brain implementation in Clojure. And so it happened that briefly before this I have decided to devote some of my time to programming in Common Lisp. What a lucky coincidence – this looks like a perfect job to swap Common Lisp back into the operational area of my brain.

You see, implementing Brian's Brain is easy. So easy that it is not worthy of a blog post except if one spices it up with some orthogonal material. The reference blog entry mentioned above does just that: implement something simple to tell everybody how cool some features of Clojure are. (And then tell that those features come at a drastic performance price.) I smell a recipe for a successful first blog entry: controversy! And the best harmless controversy one can get on the internet is apples to oranges comparisons.

So, as you might expect I'm going to compare the Clojure and Common Lisp implementations¹ of Brian's Brain. And today I'll give you some numbers about the Clojure implementations (both original and transient). And to make apples and oranges more similar I'm going to leave only the cell simulation code, leaving graphics and rendering out of the discussion. For a while.

The simulation and measuring is going to be simple: I'll measure the time it takes to simulate brains of various sizes for a set number of iterations. Since it is apparent that the time to advance the state of brain one step is proportional to the size of the brain, it is reasonable to expect the time spent to increase proportionally to the number of cells in the brain. And since all of the brain's cells are the same, there is nothing interesting to expect in the resulting numbers.

The only interesting thing I'd expect from varying brain sizes is the impact of runtime's memory management and maybe cache locality effects. Looking at these things is also interesting because the brain representation in both Lau's implementations are different: [lazy] lists in the original version and a vector in the transient version. Therefore I'll run the code for brains of different sizes, but adjusting the number of simulation steps so that the number of cells processed stays the same. This way I'd expect graphs be more-or-less straight horizontal.

The code to run simulation, nothing complicated:

(defn simulate [steps initial f]
  (loop [n steps, brain initial]
    (if (< 0 n)
      (recur (dec n) (step brain f))
      brain)))

This is a typical Clojure loop that has two "state" variables, which are updated on each iteration (by means of recur invocation): n is decreased, and brain is "transformed" using the step function. That is, on each iteration of the loop new values for these two variables are used; no variables (or values) are really modified.

The value of f is either map or pmap. This way it is easy to run a simulation in serial or parallel fasion by just passing a different function to the simulation. The original step function accepts only a single parameter:

(defn step [board]
  (doall
   (map (fn [window]
          (apply #(doall (apply map rules %&))
                 (doall (map torus-window window))))
        (torus-window board))))

In his article Lau suggests that to get the parallel version of this function only one function call must be changed. Except that after the change the function must be recompiled. Contrast this to my changed version:

(defn step [board f]
  (doall
   (f (fn [window]
        (apply #(doall (apply map rules %&))
               (doall (map torus-window window))))
      (torus-window board))))

Now nothing must be recompiled when we decide to change this function from serial to parallel version.

Another thing I had to change is how the initial brain is created. Lau uses global variables quite a lot (and we'll see how it hurts on many occassions ahead). Besides not being a nice thing in general, it also is very un-lispy (and un-functional as well, but I'll have an article on this some other time). There is nothing in Lau's code that requires global variables, so I re-wrote his code to get rid of them.

This code:

(def dim-board [90 90])

(def board
     (for [x (range (dim-board 0))]
       (for [y (range (dim-board 1))]
         [(if (< 50 (rand-int 100)) :on :off) x y])))

now has become this:

(defn make-random-board [w h]
  (for [x (range w)]
    (for [y (range h)]
      [(if (< 50 (rand-int 100)) :on :off) x y])))

Now we're ready to experiment with various combinations of brain size and iteration counts in the REPL (manually-reformatted by me for aesthetic reasons):

user> (simulate 0 (make-random-board 4 3) map)
(([:on  0 0] [:on  0 1] [:on  0 2])
 ([:on  1 0] [:on  1 1] [:off 1 2])
 ([:on  2 0] [:off 2 1] [:off 2 2])
 ([:off 3 0] [:off 3 1] [:on  3 2]))
user> (simulate 1 (make-random-board 4 3) pmap)
(([:off   0 0] [:dying 0 1] [:off   0 2])
 ([:off   1 0] [:dying 1 1] [:dying 1 2])
 ([:dying 2 0] [:off   2 1] [:off   2 2])
 ([:dying 3 0] [:dying 3 1] [:off   3 2]))
user> (simulate 2 (make-random-board 4 3) map)
(([:off 0 0] [:off 0 1] [:off 0 2])
 ([:off 1 0] [:off 1 1] [:off 1 2])
 ([:off 2 0] [:off 2 1] [:off 2 2])
 ([:off 3 0] [:off 3 1] [:off 3 2]))

One interesting observation: the board after 2 iterations looks broken (all cells are dead). Is the code somehow broken? Things like these are easy to find out interactively. But only if it's easy to specify various parameters. And that's where the global variables make life hard. In Lau's implementation, for each of the little REPL tests I'd have to go and redefine two global variables (in order). In my version one can play to their heart content without leaving the REPL.

So, what exactly is going on here? Nothing special: having half the brain's cells alive at the start makes this little brain overpopulated and by the rules of the world all cells die. And since I'm not going to manually perform pretty-printing or write a function to do it for me, I'll show another advantage of avoiding unnecessary global variables.

You see, for doing reliable experiments (like this one I'm doing here) they must be repeatable. So using randomly-initialised brains is not going to work (unless a specific pseudo-random-number-generator is seeded with some known seed, but that's besides the point). And it so happens that the other Lau's implementation uses a specific initial brain setup: two adjacent cells in the first row are initially alive. The code to create such a brain is:

(defn make-special-board [w h]
  (let [mid (/ w 2)]
   (for [x (range w)]
     (for [y (range h)]
       [(if (and (= y 0) (<= mid x (inc mid))) :on :off) x y]))))

Now, let's play a bit in the REPL:

user> (simulate 0 (make-special-board 4 3) map)
(([:off 0 0] [:off 0 1] [:off 0 2])
 ([:off 1 0] [:off 1 1] [:off 1 2])
 ([:on  2 0] [:off 2 1] [:off 2 2])
 ([:on  3 0] [:off 3 1] [:off 3 2]))
user> (simulate 1 (make-special-board 4 3) map)
(([:off   0 0] [:off 0 1] [:off 0 2])
 ([:off   1 0] [:off 1 1] [:off 1 2])
 ([:dying 2 0] [:on  2 1] [:on  2 2])
 ([:dying 3 0] [:on  3 1] [:on  3 2]))
user> (simulate 2 (make-special-board 4 3) map)
(([:on  0 0] [:on    0 1] [:on    0 2])
 ([:on  1 0] [:on    1 1] [:on    1 2])
 ([:off 2 0] [:dying 2 1] [:dying 2 2])
 ([:off 3 0] [:dying 3 1] [:dying 3 2]))
user> (= *1 (simulate 2 (make-special-board 4 3) pmap))
true
user> (= (simulate 10 (make-special-board 32 32) map)
         (simulate 10 (make-special-board 32 32) pmap))
true

Great, not only can we experiment with different brain dimensions but also with different contents. And we can easily check if parallel and sequential versions work the same. Now try doing this in the Lau's original version!

Now we are almost ready to measure things. Here's the function I'll use:

(defn benchmark []
  ;; Warmup
  (simulate 7500 (make-special-board 16 16) map)
  (simulate 7500 (make-special-board 16 16) pmap)
  (println (clojure-version))
  (doseq [[w h i] [[32    32  32768]
                   [64    64  8192]
                   [128  128  2048]
                   [256  256  512]
                   [512  512  128]]]
    (let [initial (doall (make-special-board w h))]
      (print (str "S " w "x" h ", " i " iteration(s): "))
      (time (simulate i initial map))
      (flush)
      (print (str "P " w "x" h ", " i " iteration(s): "))
      (time (simulate i initial pmap))
      (flush))))

Nothing special, repeat serial and parallel versions for given brain dimensions and iteration number. The results of running this on my MacBook Pro² (with the warmup timings removed):

Running this benchmark from shell can be done like this:

$ java -server -jar clojure.jar -i ca.clj -e "(benchmark)"

After a while of intensive contributing to the global warming we get some output:

$ java -server -jar clojure.jar -i ca.clj -e "(benchmark)"
1.1.0-alpha-SNAPSHOT
S 32x32, 32768 iteration(s): "Elapsed time: 415506.172 msecs"
P 32x32, 32768 iteration(s): "Elapsed time: 289353.533 msecs"
S 64x64, 8192 iteration(s): "Elapsed time: 425244.632 msecs"
P 64x64, 8192 iteration(s): "Elapsed time: 290253.746 msecs"
S 128x128, 2048 iteration(s): "Elapsed time: 421812.085 msecs"
P 128x128, 2048 iteration(s): "Elapsed time: 287244.863 msecs"
S 256x256, 512 iteration(s): "Elapsed time: 422331.897 msecs"
P 256x256, 512 iteration(s): "Elapsed time: 289623.448 msecs"
S 512x512, 128 iteration(s): "Elapsed time: 440064.214 msecs"
P 512x512, 128 iteration(s): "Elapsed time: 286282.461 msecs"

One thing you might have noticed is that the number of iterations increases as the brain size decreases. This is to have the number of cells processed in each simulation constant and the resulting numbers easy to compare.

I also run all the "benchmarks" on two JVMs (server VMs at that): OSX default 1.5 (32-bit) and 1.6 (64-bit, there's only server VM). The switching is done using the Java Preferences utility:

$ java -version
java version "1.5.0_20"
Java(TM) 2 Runtime Environment, Standard Edition (build 1.5.0_20-b02-315)
Java HotSpot(TM) Client VM (build 1.5.0_20-141, mixed mode, sharing)

$ java -server -version
java version "1.5.0_20"
Java(TM) 2 Runtime Environment, Standard Edition (build 1.5.0_20-b02-315)
Java HotSpot(TM) Server VM (build 1.5.0_20-141, mixed mode)

$ java -version
java version "1.6.0_15"
Java(TM) SE Runtime Environment (build 1.6.0_15-b03-226)
Java HotSpot(TM) 64-Bit Server VM (build 14.1-b02-92, mixed mode)

Here are the numbers for the original Brian's Brain implementation:

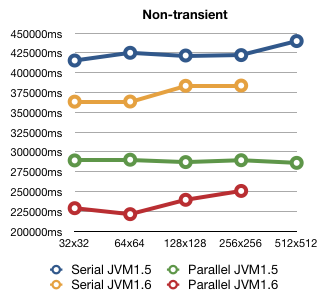
Looks like the parallel version is about 45% (JVM1.5) to 60% (JVM1.6) faster than the serial.

The times for 512x512 are not included for JVM1.6 because the serial version was running for 2416341.265ms (that's about 40 minutes!), which is way out of scale for this graph. I guess it is because of tight memory situation because the next (parallel) benchmark bailed out with out of memory exception.

Lau's code for transient version is much worse. More global variables. And functions depending on them. What a mess… Just look at it:

(def dim-board   [130  130])
(def dim-screen  [600  600])
(def dim-scale   (vec (map / dim-screen dim-board)))

(def board-size (apply * dim-board))
(def board      (-> (vec (repeat board-size :off))
                    (assoc (/ (dim-board 0) 2)       :on)
                    (assoc (inc (/ (dim-board 0) 2)) :on)))

(def cords (for [y (range (dim-board 0)) x (range (dim-board 1))] [x y]))

(defn torus-coordinate
  [idx]
  (cond (neg? idx)          (+ idx board-size)
        (>= idx board-size) (- idx board-size)
    :else idx))

(def above     (- (dim-board 0)))
(def below     (dim-board 0))
(def neighbors [-1 1 (dec above) above (inc above) (dec below) below (inc below)])

(defn on-neighbors [i board]
  (count
   (filter #(= :on (nth board %))
           (map #(torus-coordinate (+ i %)) neighbors))))

(defn step [board]
  (loop [i 0 next-state (transient board)]
    (if (< i board-size)
      (let [self         (nth board i)]
        (recur (inc i)
               (assoc! next-state i (cond
                                      (= :on    self)                :dying
                                      (= :dying self)                :off
                                      (= 2 (on-neighbors i board))   :on
                                      :else                          :off))))
      (persistent! next-state))))

9 global variables in 37 lines of code! Bad Lau! Bad! Also, the results of torus-coordinate, on-neighbors and step (in short – all of them) depend on things besides the parameters. Very un-functional indeed.

Ok, let's put horrors aside and do what we can to get this mess under control. My only goal is to get the simulation and benchmarking functions working, so first, here they are:

(defn simulate [steps initial]
  (loop [n steps, board initial]
    (if (< 0 n)
      (recur (dec n) (step board))
      board)))

(defn benchmark []
  ;; Warmup
  (simulate 10000 (make-board 16 16))
  (println (clojure-version))
  (doseq [[w h i] [[32    32  32768]
                   [64    64  8192]
                   [128  128  2048]
                   [256  256  512]
                   [512  512  128]
                   [1024 1024 32]]]
    (let [initial (make-board w h)]
      (print (str "S " w "x" h ", " i " iteration(s): "))
      (time (simulate i initial))
      (flush))))

Notice that the transient version cannot be parallelized by simply changing a single function, so there is no parallel version at all.

Here's the changed code that allows me to run the benchmark:

(defn make-board [w h]
  (let [above (- w), below w]
    (def neighbors [-1 1 (dec above) above (inc above) (dec below) below (inc below)]))

  (-> (vec (repeat (* w h) :off))
      (assoc (/ w 2)       :on)
      (assoc (inc (/ w 2)) :on)))

(defn torus-coordinate [idx board]
  (let [board-size (count board)]
    (cond (neg? idx)          (+ idx board-size)
          (>= idx board-size) (- idx board-size)
          :else idx)))

(defn on-neighbors [i board]
  (count
   (filter #(= :on (nth board %))
           (map #(torus-coordinate (+ i %) board) neighbors))))

(defn step [board]
  (let [board-size (count board)]
    (loop [i 0 next-state (transient board)]
      (if (< i board-size)
        (let [self         (nth board i)]
          (recur (inc i)
                 (assoc! next-state i (cond
                                       (= :on    self)                :dying
                                       (= :dying self)                :off
                                       (= 2 (on-neighbors i board))   :on
                                       :else                          :off))))
        (persistent! next-state)))))

make-board is ugly, and defines global variables. Will have to live with it. torus-coordinate and step don't use global variables any more. And we're down to one global variable which on-neighbors depends on. I'll let this one remain on Lau's conscience.

Another thing that I just can't let slip is that the torus-coordinate function is JUST PLAIN WRONG. Sorry, I might have raised my voice. The problem is that for the cell in the leftmost column the cell to its left is on the opposite side of the board. Similarly for the rightmost. But torus-coordinate cheats and for the leftmost returns the cell on the rightmost column (correct) but one row above (wrong!). For the rightmost cells it returns the cell on the leftmost column, but one row below. This error would instantly disqualify the transient implementation in any half-serious apples-to-apples comparison.

It is easy to see that torus-coordinate is called for every "off" cell in a brain. And there are more "off" cells than "dying" or "on" or the sum of those, respectively (based on my observations of running the simulations graphically; empirical proof is easy, but will have to wait). Allowing this function to do less work definitely impacts its performance. I'm not going to write the correct Clojure version of this function so let's pretend everything is just fine and look at the performance:

$ java -server -jar clojure.jar -i transient-ca.clj -e "(benchmark)"
1.1.0-alpha-SNAPSHOT
S 32x32, 32768 iteration(s): "Elapsed time: 68259.648 msecs"
S 64x64, 8192 iteration(s): "Elapsed time: 69464.992 msecs"
S 128x128, 2048 iteration(s): "Elapsed time: 67646.623 msecs"
S 256x256, 512 iteration(s): "Elapsed time: 70889.975 msecs"
S 512x512, 128 iteration(s): "Elapsed time: 72941.713 msecs"
S 1024x1024, 32 iteration(s): "Elapsed time: 73866.637 msecs"

Quite an improvement I'd say, indeed. And since the benchmark finished relatively fast, I decided to run it again:

$ java -server -jar clojure.jar -i transient-ca.clj -e "(benchmark)"
1.1.0-alpha-SNAPSHOT
S 32x32, 32768 iteration(s): "Elapsed time: 90808.629 msecs"
S 64x64, 8192 iteration(s): "Elapsed time: 92661.493 msecs"
S 128x128, 2048 iteration(s): "Elapsed time: 89570.418 msecs"
S 256x256, 512 iteration(s): "Elapsed time: 92398.728 msecs"
S 512x512, 128 iteration(s): "Elapsed time: 94843.865 msecs"
S 1024x1024, 32 iteration(s): "Elapsed time: 97478.63 msecs"

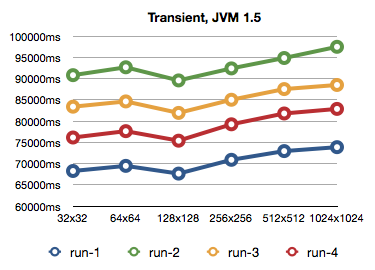
Weird is the least I can say about this. So I run it one more time… And then again. All the times getting different timings (I was not doing anything else while running the benchmarks on the computer, so I don't have a slightest clue about the cause of variation). Then I gave up. Here's a graph of all four runs:

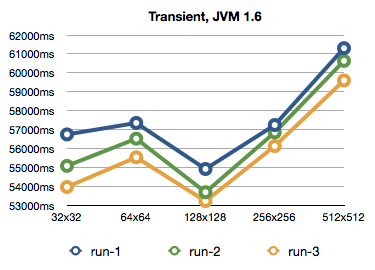
Three more runs on JVM1.6, which are quite a bit faster and closer to each other. But they run out of memory on the 1024x1024 run.

Here are the averages of all the runs together in one graph:

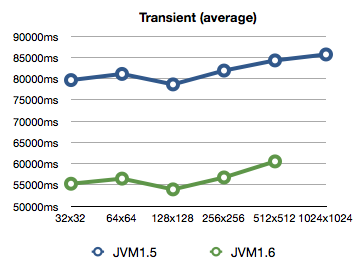
Around 25% speed increase in JVM1.6 if I'm reading the numbers correctly.

Now, the complete picture of original and transient implementations:

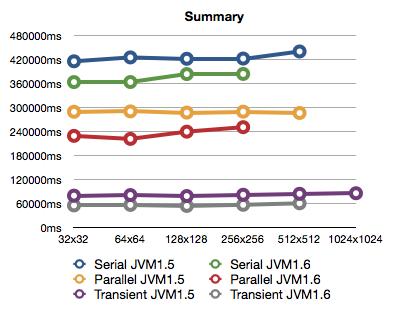
As expected the lines are quite horizontal, but not in all cases. Especially non-horizontal are the original implementation on the JVM1.6. It might be related to it being 64-bit, but I'm not really going to investigate this any further. So, as we can see, the transient version is about 4 times faster than the parallel original version, and about 6 times faster than serial version.

It is apparent that the transient version is quite a bit faster than the original. And with the original version we can see that the parallel version really does speed things up on two cores. How about 8 cores? It so happens that I have SSH access to a quite recent Mac Pro³. One notable thing about this system is that it is set to energy-saving mode, so don't be surprised by the absolute numbers, look for their relative magnitudes:

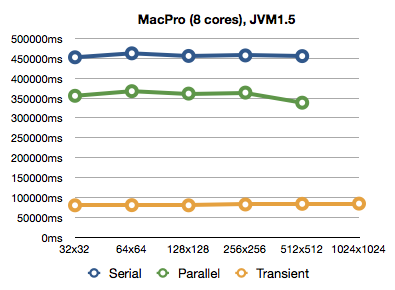
Watching the java process in top was showing around 600% CPU usage when running the parallel simulations. What surprises me is that the performance gain from more cores is not there. But surprise is not big enough for me to go investigate this any further.

This is only an introduction for what I really wanted to write about. It turned out much longer than I thought it would be. Cangratulations to everybody who got this far (reading the content, not searching for pretty pictures).

This article is in no way intended as bashing on anything. Yes, I didsagree with Lau on some software design points, but that should be only considered as that – disagreement. I have shown how I'd write some parts of his program. He will be welcome to comment on my Common Lisp implementation after my next post.

Please don't use these numbers to draw any conclusions about the performance of my computer, Clojure, Java, my or Lau's code or anything else. The numbers are as un-scientific as can be. I was intentionally not doing anyhting else while running the benchmarks on the computer, but there are all the usual desktop things running (except the screensaver which I disabled).

Original: source MacBook Pro transcript MacPro transcript
Transient: source MacBook Pro transcript MacPro transcript

Apparently I have been misguided about the energy-savings mode on the MacPro. Going to the box physically and checking if the option is turned on or not, I found out (to my big surprise) that the option is gone. For those who have a Mac can compare their "Energy Saver" window to what it was like before: http://support.apple.com/kb/HT3092. So, I'm not sure whether the "reduced" mode is enabled or not.