Brian's brain, on Common Lisp
The real thing
If you are reading this you might have already read the previous entry and are familiar with the problem domain. And today I'm going to walk you through implementing Brian's Brain in Common Lisp. First, the straight-forward implementation with brain represented as a 2-dimensional array (that's what it is, right?), with just enough code to get it running. There are no functions to abstract away the brain implementation details or cell representation or anything else.
First, a function to create a brain:
(defun make-brain (w h) (make-array (list h w) :initial-element :off))
And another function that will make us an initialised brain (like the one in Clojure version):
(defun make-initialised-brain (w h) (let ((cells (make-brain w h)) (mid (floor w 2))) (setf (aref cells 0 mid) :on) (setf (aref cells 0 (1+ mid)) :on) cells))
Why are the dimensions to make-array passed as (h w) and not (w h) you might ask? Because I
like to see that my functions work as soon as I write them. Let's see how it works:
CL-USER> (make-initialised-brain 7 5)
#2A((:OFF :OFF :OFF :ON :ON :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF :OFF :OFF))
What would happen if we had them in the opposite order:
CL-USER> (make-initialised-brain 5 7)
#2A((:OFF :OFF :ON :ON :OFF)
(:OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF))
Incidentally, this is how Lau's version has them (if you have followed the examples carefully enough). There is no real difference having them either way, only a matter of convenience: if I look at the brain in REPL I want to see the same thing I'd see in animated graphical output.
The rules are independent of brain representation as long as we can provide the neighbouring cells as a parameter:
(defun rules (state neighbours) (case state (:on :dying) (:dying :off) (t (if (= 2 (count :on neighbours)) :on :off))))
How do we find the neighbours of a given cell? Easy, like this:
(defun neighbours (cells x y) (let* ((mx (1- (array-dimension cells 1))) (my (1- (array-dimension cells 0))) (l (if (zerop x) mx (1- x))) (r (if (= x mx) 0 (1+ x))) (u (if (zerop y) my (1- y))) (d (if (= y my) 0 (1+ y)))) (mapcar (lambda (x y) (aref cells y x)) (list l x r l r l x r) (list u u u y y d d d))))
What happens here should be pretty obvious, but I'll explain a bit anyway since this is a one-way
communication channel. mx and my are maximal values for x and y coordinates. Left of the
cell (l) is current x coordinate minus 1, unless we're on the leftmost column (0), in which
case we get mx. Similarly for right cell, except we look if we're on the rightmost column (mx),
and wrap to 0 if we are. Similarly for y axis. In short, referencing a cell off the edge gets
us a cell on the opposite side.
Then for each pair of coordinates around our cell we get the value from the cells array. These
pairs are given by two lists: one fore x coordinates and one for y coordinates. Function
mapcar goes over both lists simultaneously and applies given function to each successive pair of
items from both lists.
Also note how indices are passed to aref, with y and x in unnatural positions. This is for
the reasons explained above – the rows are first dimension, and columns the second. But
neighbours function expects them in the natural order, leaving the implementation details out of
the way.
Let's check if our neighbours function works as expected:
CL-USER> (neighbours (make-initialised-brain 7 5) 3 4) (:OFF :OFF :OFF :OFF :OFF :OFF :ON :ON)
The resulting list is cell values for, respectively, left-up, up, right-up, left, right, left-down,
down and right-down cells from the specified x, y coordinate.
What's left? Evolution. The function which will create next state of a brain:
(defun evolve (src) (let* ((w (array-dimension src 1)) (h (array-dimension src 0)) (dst (make-brain w h))) (loop for j below h do (loop for i below w do (setf (aref dst j i) (funcall 'rules (aref src j i) (neighbours src i j))))) dst))
Ordinary loop over rows and columns, setting values in newly created brain by applying the rules
to a cell and its neighbours in the current brain. We're ready to play now:
CL-USER> (evolve (make-initialised-brain 7 5))
#2A((:OFF :OFF :OFF :DYING :DYING :OFF :OFF)
(:OFF :OFF :OFF :ON :ON :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :OFF :OFF :OFF :OFF)
(:OFF :OFF :OFF :ON :ON :OFF :OFF))
CL-USER> (evolve *)
#2A((:OFF :OFF :ON :OFF :OFF :ON :OFF)
(:OFF :OFF :OFF :DYING :DYING :OFF :OFF)
(:OFF :OFF :OFF :ON :ON :OFF :OFF)
(:OFF :OFF :OFF :ON :ON :OFF :OFF)
(:OFF :OFF :OFF :DYING :DYING :OFF :OFF))
Using numbers for cell values would be much better visually, but I'm staying close to the Clojure version (for now).
Getting ready for blastoff
Almost ready to do some timing. All we need are the simulate and benchmark functions:
(defun simulate (steps initial) (loop repeat steps for brain = initial then (funcall 'evolve brain) finally (return brain))) (defun benchmark () (format *trace-output* "Benchmarking on ~A ~A~%" (lisp-implementation-type) (lisp-implementation-version)) ;; Warmup. (simulate 10000 (make-initialised-brain 16 16)) (loop for (w h i) in '((32 32 32768) (64 64 8192) (128 128 2048) (256 256 512) (512 512 128) (1024 1024 32) (2048 2048 8) (4096 4096 2)) do (let ((initial (make-initialised-brain w h))) (format *trace-output* "*** ~Dx~D ~D iteration~:P ***~%" w h i) (time (simulate i initial)) (finish-output *trace-output*))) (values))
Notice that there is not a single type annotation in this code. Running it on my laptop1:
CL-USER> (benchmark) Benchmarking on SBCL 1.0.31.32 *** 32x32 32768 iterations *** Evaluation took: 34.782 seconds of real time 34.064263 seconds of total run time (33.060215 user, 1.004048 system) [ Run times consist of 7.670 seconds GC time, and 26.395 seconds non-GC time. ] 97.94% CPU 96,906,498,234 processor cycles 14,769,770,512 bytes consed *** 64x64 8192 iterations *** Evaluation took: 33.512 seconds of real time 32.776229 seconds of total run time (31.254474 user, 1.521755 system) [ Run times consist of 5.903 seconds GC time, and 26.874 seconds non-GC time. ] 97.80% CPU 93,366,482,790 processor cycles 14,762,592,768 bytes consed ... snipped
Running from the terminal would look something like this:
$ sbcl --noinform --disable-debugger --load simple.fasl --eval "(benchmark)" --eval "(quit)"
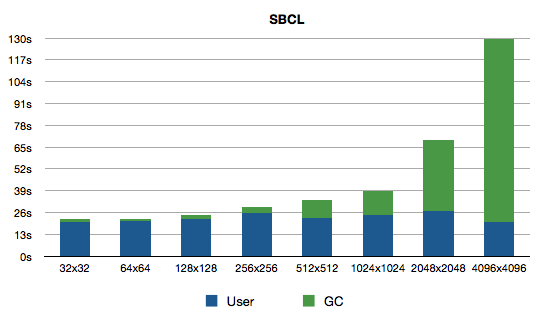
This time we have more information to display in the graphs: total run time and GC time. And just look at the numbers:
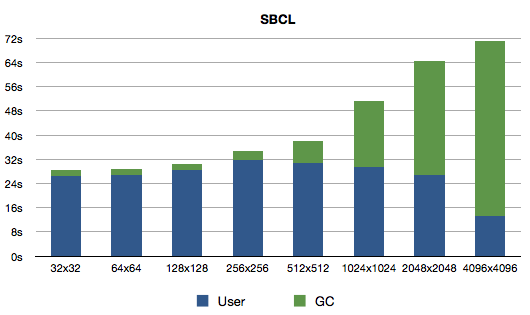
Interesting. Very interesting, indeed. What we see here is that the time to run one iteration (blue bars) is increasing a bit first and then declines quite sharply. GC time (green), on the other hand, increases quite sharply starting from 256x256 simulation. Can you come up with an explanation?
I have one. Smaller arrays are processed quite fast, so are short lived, and become garbage before GC kicks in. The bigger arrays are processed longer, so they are alive when GC starts. And GC has to walk all array elements each time, since arrays are not specialised (that is, can contain anything). I told you using numbers would be better (for different reasons, though)!
I also did another run of this same benchmark (transcripts available below), and the numbers were the same up to sub-second precision.
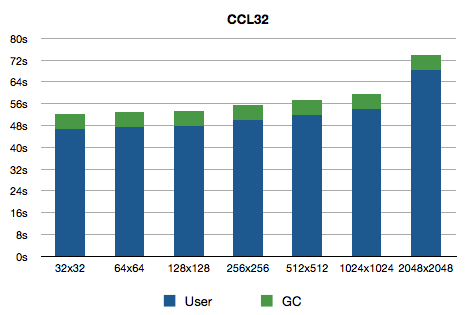
Let's do this same thing with a different Common Lisp implementation, which in my case will be Clozure CL. The nice thing about this implementation that its compiler is very snappy. Running from shell looks like this:
$ ccl -n -Q -l simple.dx32fsl -e "(benchmark)"
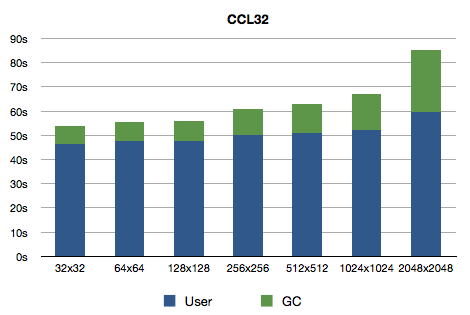
One thing to note is that arrays of size 4096x4096 exceed the limit of array length (24-bit number) of 32-bit Clozure CL, which, coincidentally, is just 1 short of what we need:
CL-USER> array-dimension-limit 16777216 CL-USER> (integer-length array-dimension-limit) 25 CL-USER> (integer-length (1- array-dimension-limit)) 24 CL-USER> (* 4096 4096) 16777216
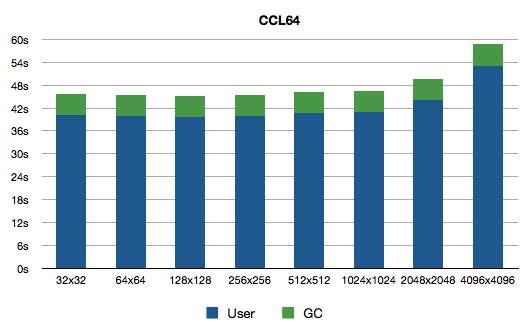
But otherwise there is less variation in 32-bit Clozure CL. Let's look at 64-bit version:
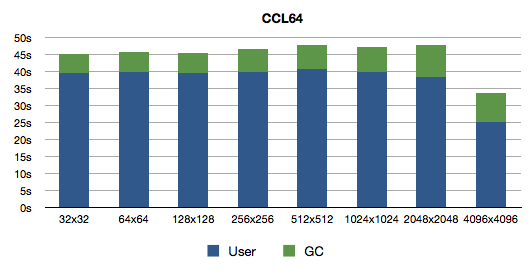
Nice, behaviour similar to SBCL, except that GC times don't grow as fast.
Missing things
I hear somebody in the corner mumbling something about animation and graphics. Oh, right. Missed that one. But it so happens that the very thing that made me start playing with Brian's Brain is that I installed cl-opengl. And guess what? It worked right out of the box. On all the Common Lisp implementation I have on my computer. So I had to start playing with it. And the rest, as they say, is history.
It works like this:
CL-USER> (asdf:operate 'asdf:load-op :cl-glut-examples) ; System loading output snipped... NIL CL-USER> (cl-glut-examples:run-examples)
And all the examples pop up, many of them animating. So I peek at some examples to see how to set up a window. Easy as a pie:
(defclass bb (glut:window) ((cells :accessor cells-of :initarg :cells)) (:default-initargs :title "Brian's Brain in CL" :mode '(:double :rgb))) (defmethod glut:display-window :before ((w bb)) (gl:clear-color 0 0 0 0) (gl:matrix-mode :projection) (gl:load-identity) (let ((cells (cells-of w))) (gl:ortho 0 (array-dimension cells 1) 0 (array-dimension cells 0) -1 1)))
Then we need a function to render a single cell at specified position. Drawing squares is easy enough:
(defun render-cell (x y cell) (flet ((draw-cell (x y) (gl:with-pushed-matrix (gl:translate x y 0) (gl:with-primitive :polygon (gl:vertex 0.1 0.1 0) (gl:vertex 0.9 0.1 0) (gl:vertex 0.9 0.9 0) (gl:vertex 0.1 0.9 0))))) (case cell (:on (gl:color 1 1 1) (draw-cell x y)) (:dying (gl:color 0.5 0.5 0.5) (draw-cell x y)))))
All that's left are some callbacks to draw the whole window and run the animation. The following two methods will do just fine:
(defmethod glut:display ((w bb)) (gl:clear :color-buffer) (let* ((cells (cells-of w)) (w (array-dimension cells 1)) (h (array-dimension cells 0))) (loop for j below h do (loop for i below w do (render-cell i j (aref cells j i))))) (glut:swap-buffers)) (defmethod glut:idle ((w bb)) (setf (cells-of w) (evolve (cells-of w))) (glut:post-redisplay))
Everything is ready now. An animated Brian's Brain can be created like this:
(glut:display-window (make-instance 'bb
:cells (make-initialised-brain 128 128)
:width 512
:height 512))
But since I don't like to put things on the toplevel which run when just loading a file, I'll put the code into a function:
(defun run (w h ww wh) (glut:display-window (make-instance 'bb :cells (make-initialised-brain w h) :width ww :height wh)))
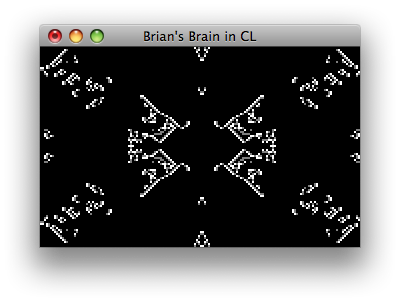
Feel free to start a never-ending Brian's Brain simulation:
CL-USER> (run 160 100 320 200)
Finishing touches
To make this all easily loadable I'll put all code in its own package and create a system definition (which nowadays means an ASDF) file. Refer to Xach's intro for a nice description of why and how to do this.
Package definition is very simple:
(defpackage :brians-brain-1 (:use :common-lisp) (:export #:run))
And the system definition is nothing complicated, either:
(asdf:defsystem :brians-brain-1 :version "1.0" :author "Jānis Džeriņš" :license "Send me money if you find this stuff useful." :depends-on (cl-opengl cl-glut) :components ((:file "package") (:file "simple" :depends-on ("package")) (:file "display" :depends-on ("package" "simple"))))
At this point we can get to a running animated Brian's Brain from the shell prompt:
$ sbcl --noinform --disable-debugger \
--eval "(asdf:operate 'asdf:load-op :brians-brain-1)" \
--eval "(brians-brain-1:run 160 100 320 200)" \
--eval "(quit)"
Looking forward
Next time I'm going to play with different brain representations.
Data files
Updates
2009-10-28: Noticed a bug in simulate function which runs the simulation for one step less than
asked. The corrected version looks like this:
(defun simulate (steps initial) (loop with brain = initial repeat steps do (setf brain (funcall 'evolve brain)) finally (return brain)))
Also now invoking GC before each simulation so that garbage from previous simulation has less chance to influence the next:
(defun benchmark () (format *trace-output* "Benchmarking on ~A ~A~%" (lisp-implementation-type) (lisp-implementation-version)) ;; Warmup. (simulate 10000 (make-initialised-brain 16 16)) (loop for (w h i) in '((32 32 32768) (64 64 8192) (128 128 2048) (256 256 512) (512 512 128) (1024 1024 32) (2048 2048 8) (4096 4096 2)) do #+ccl (gc) #+sbcl (gc :full t) (let ((initial (make-initialised-brain w h))) (format *trace-output* "*** ~Dx~D ~D iteration~:P ***~%" w h i) (time (simulate i initial)) (finish-output *trace-output*))) (values))
The graphs are generally very similar, except the rightmost columns don't look fishy:
New transcripts: